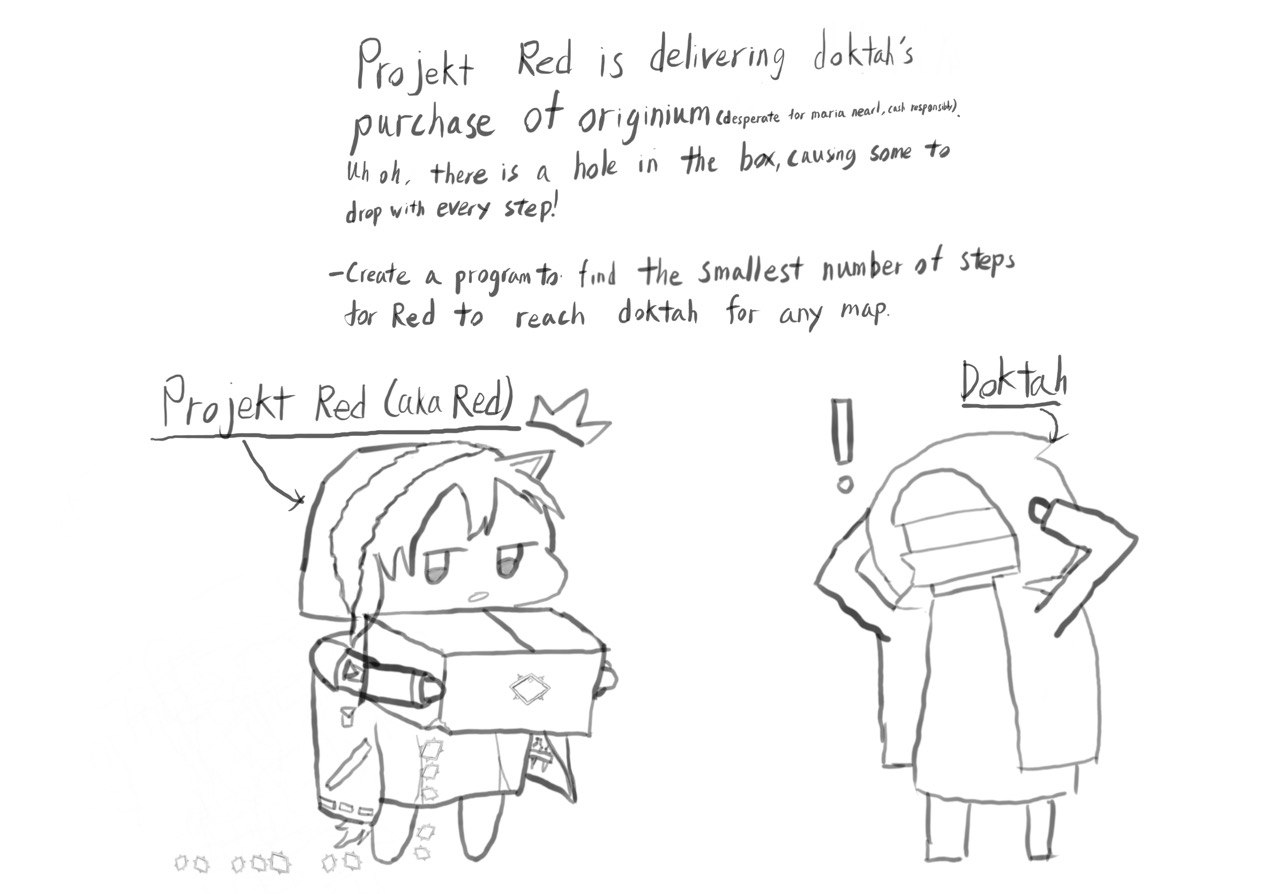
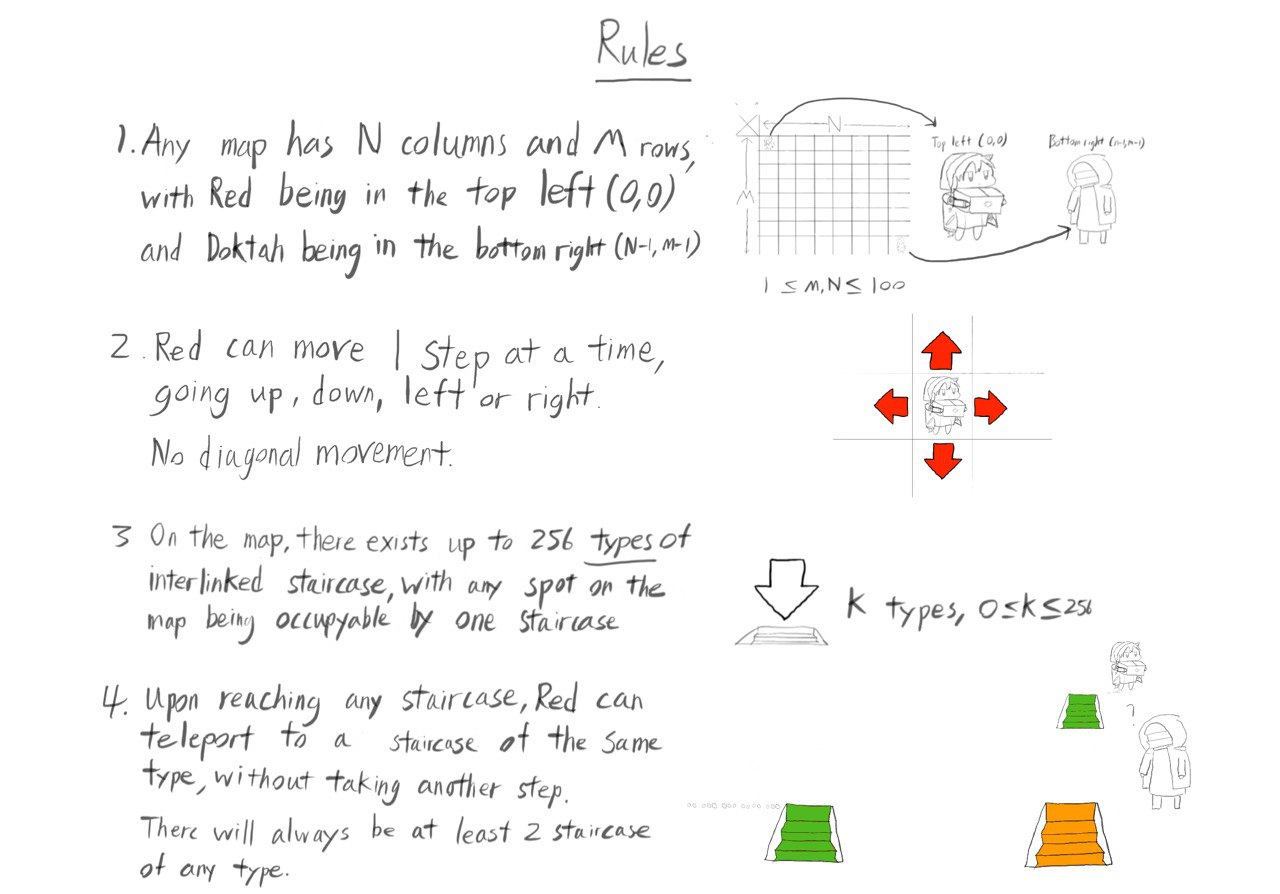
Getting from the top left to bottom right
The task:
Bob is a deliveryman and is delivering a package to his destination. He started his journey from position (0,0) and his destination is the bottom-right corner of the map.
Each step, his car can move 1 square up, down,left or right. If his car reaches a black hole, it can teleport to any other location connected to the black hole at no cost, he also can skip the teleport feature.
Find the least number of steps(shortest path) that Bob can take to move from (0,0) to the destination.
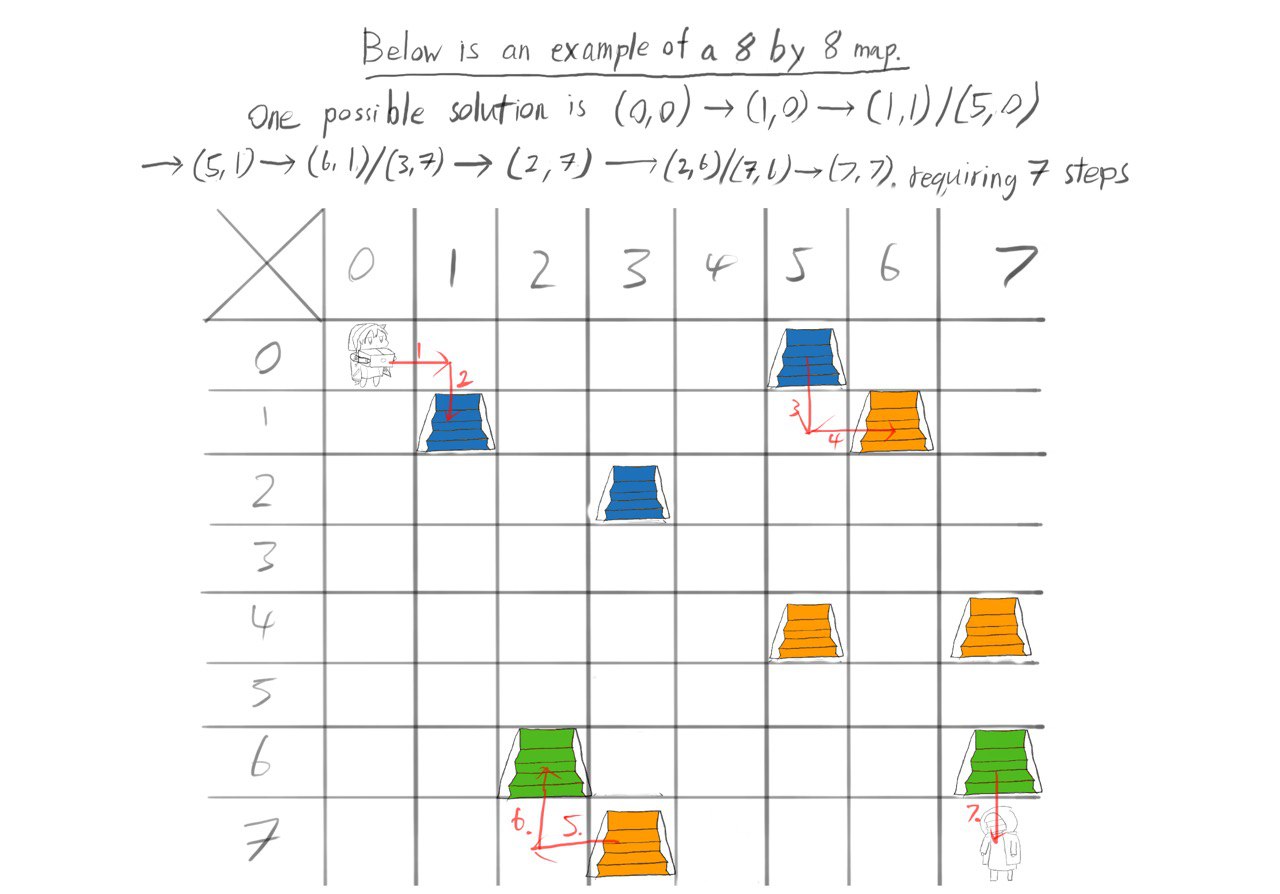
Given the complexity of the problem, a simple system with only 1 type of portal on a 3 by 3 grid was investigated by converting it into a graph in order to find ways to reduce the complexity of the problem.
The first thing that could be done was converting the map into a graph in order to see what observations could be made.
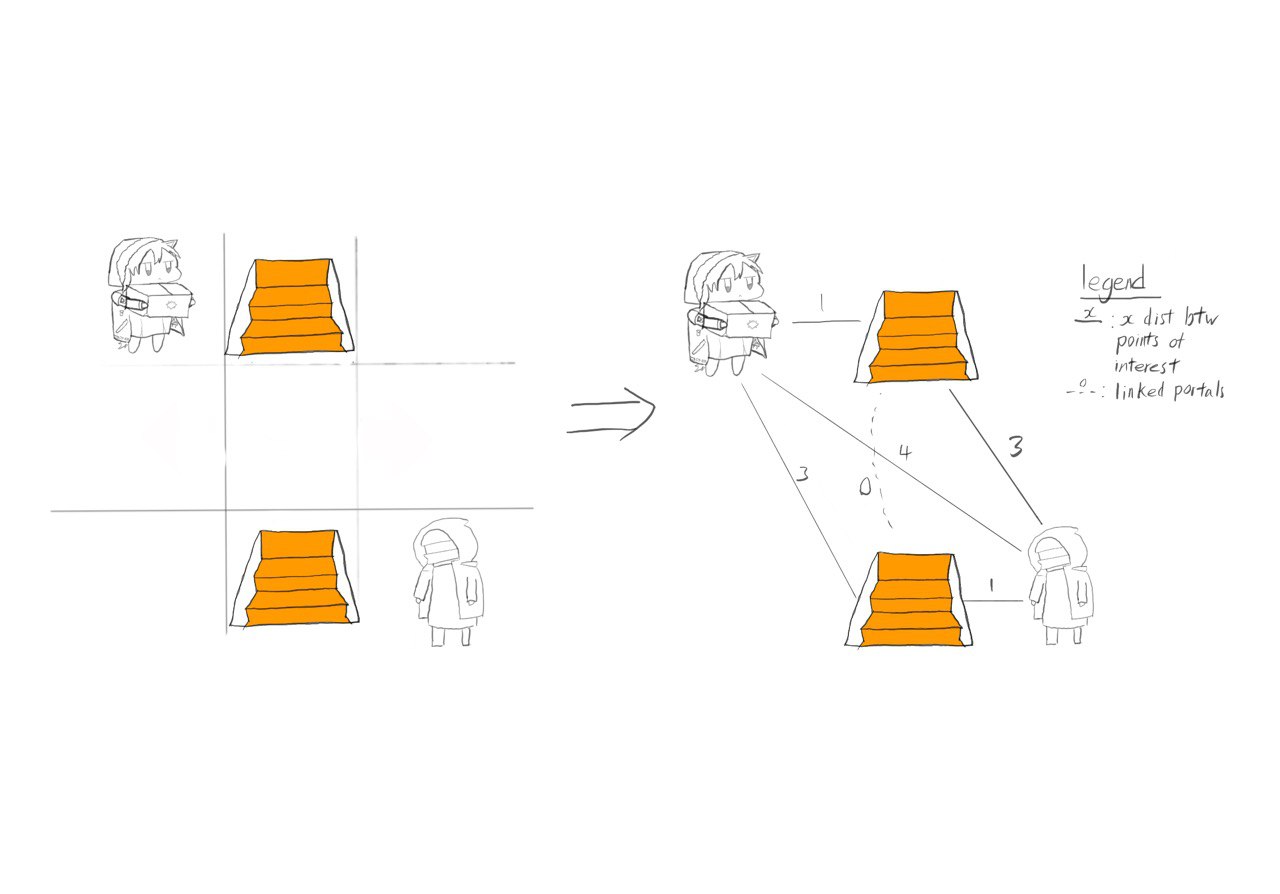
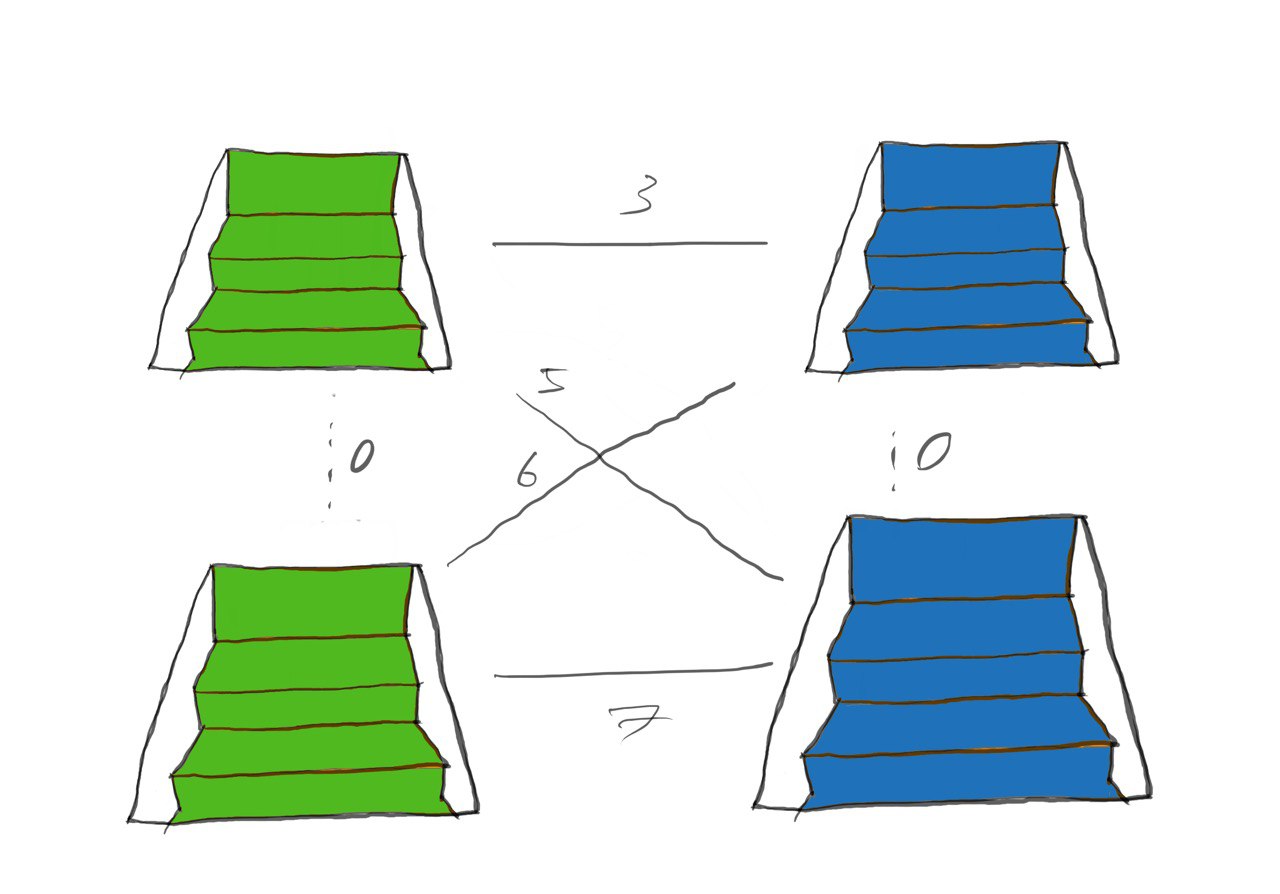
Investigating the distance between the staircases and the initial starting position, we realize that we will always use the shortest path to any staircase of that type in order to get to any staircase. Doing this again with the destination and the staircases allows us to simplify the graph, such that there are only three nodes. The start, end and the staircase.
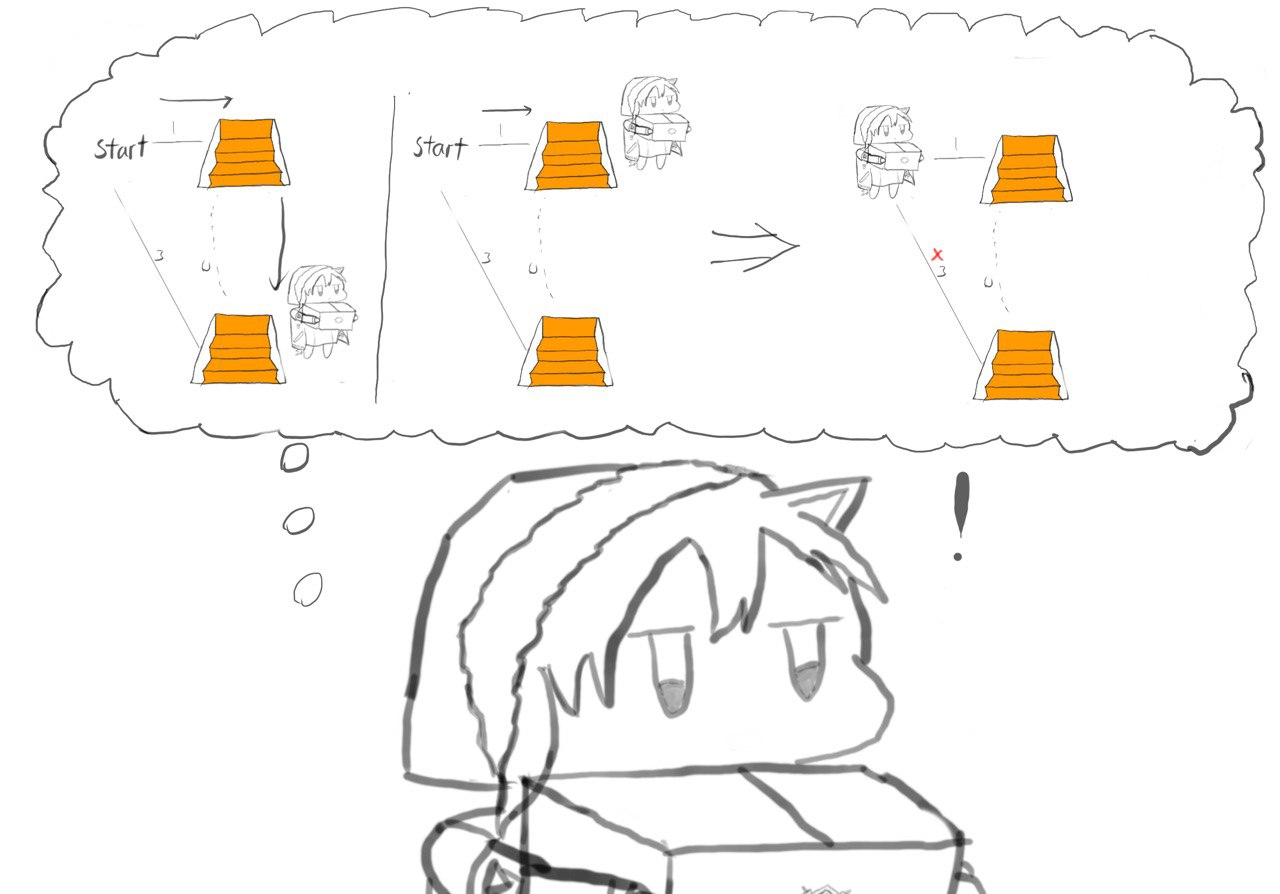
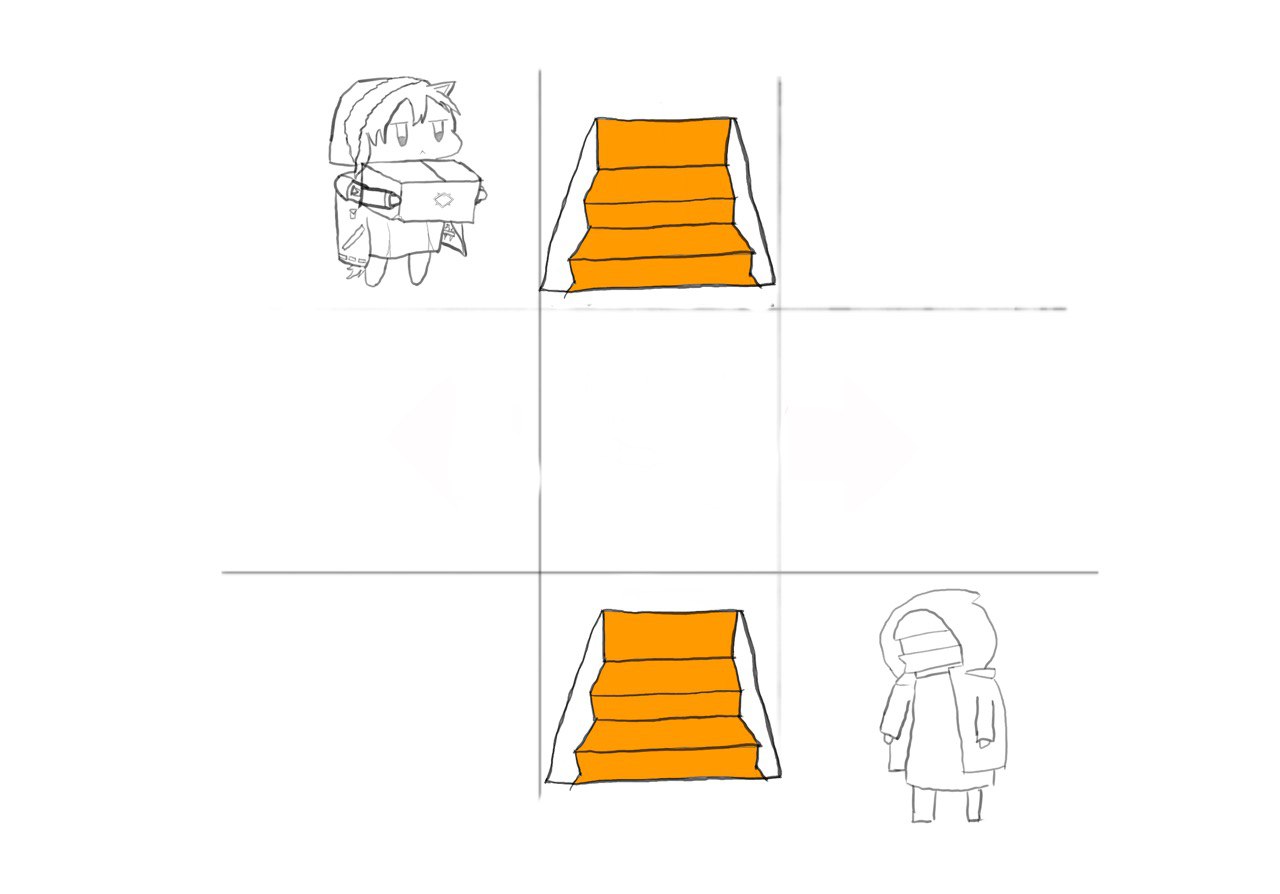
Next, we will need to observe a system with more than one type of staircase and see how we can simplify the system. Looking at the connections, we can simplify them using the same method we use once we have resolved the connections between staircase(highlighted in pink)
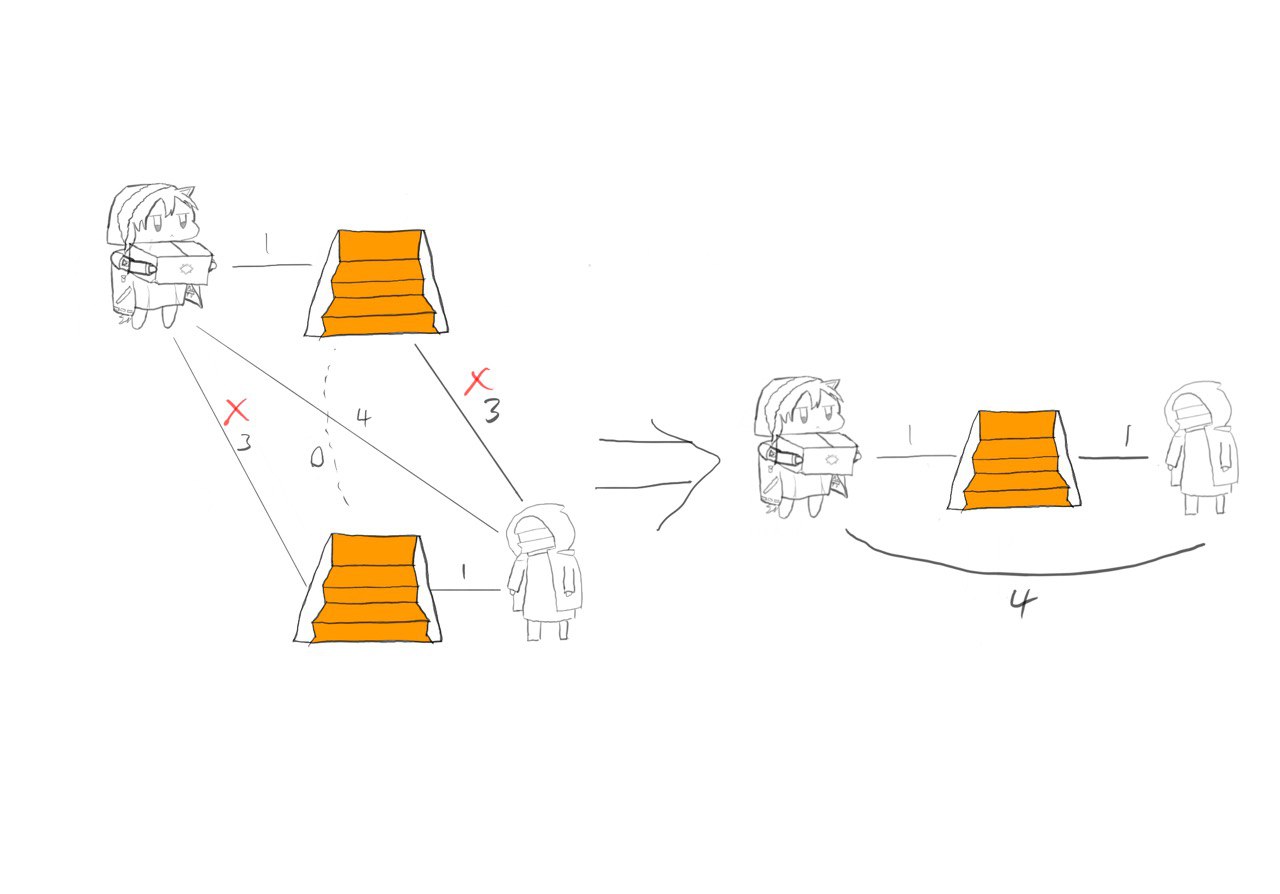
For connections between staircases, we can see that we only need to care about the shortest path between staircase of a certain type, as one would be able to teleport to the location to use the shortest path before teleporting again to any staircase that they wish to use. Combining this with what we learned from before, we are now able to simplify the system once again. The simplified graph includes four nodes, one for the start and end and one each for each type of staircase.
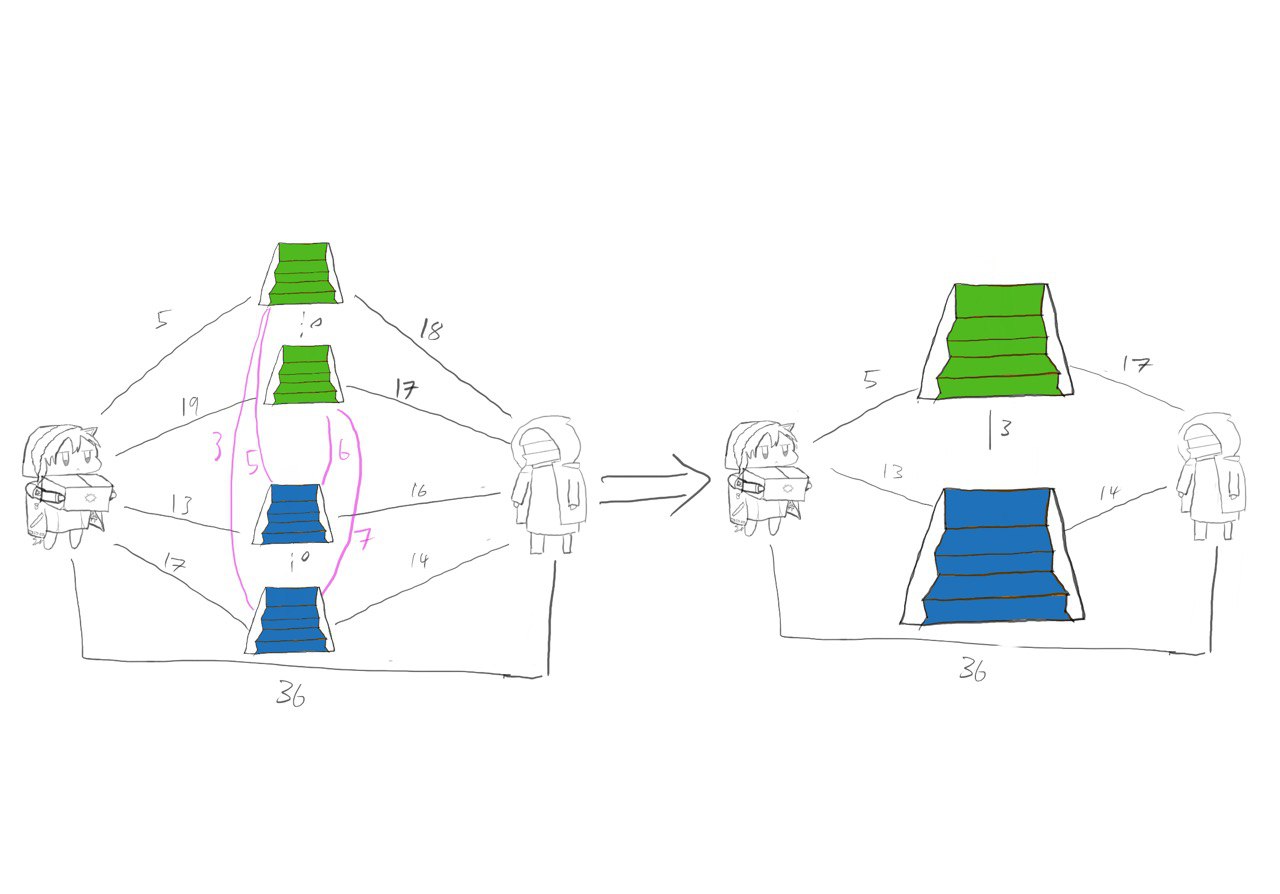
Now we can start to see a clear pattern in the reduced graph:
1. The graph will have (N+2) nodes, one for the start and end and one for each type of staircase present.
2. The distance between each node will be the shortest distance between any node of that type preesent on the map.
And that gives us the following steps to solve the problem:
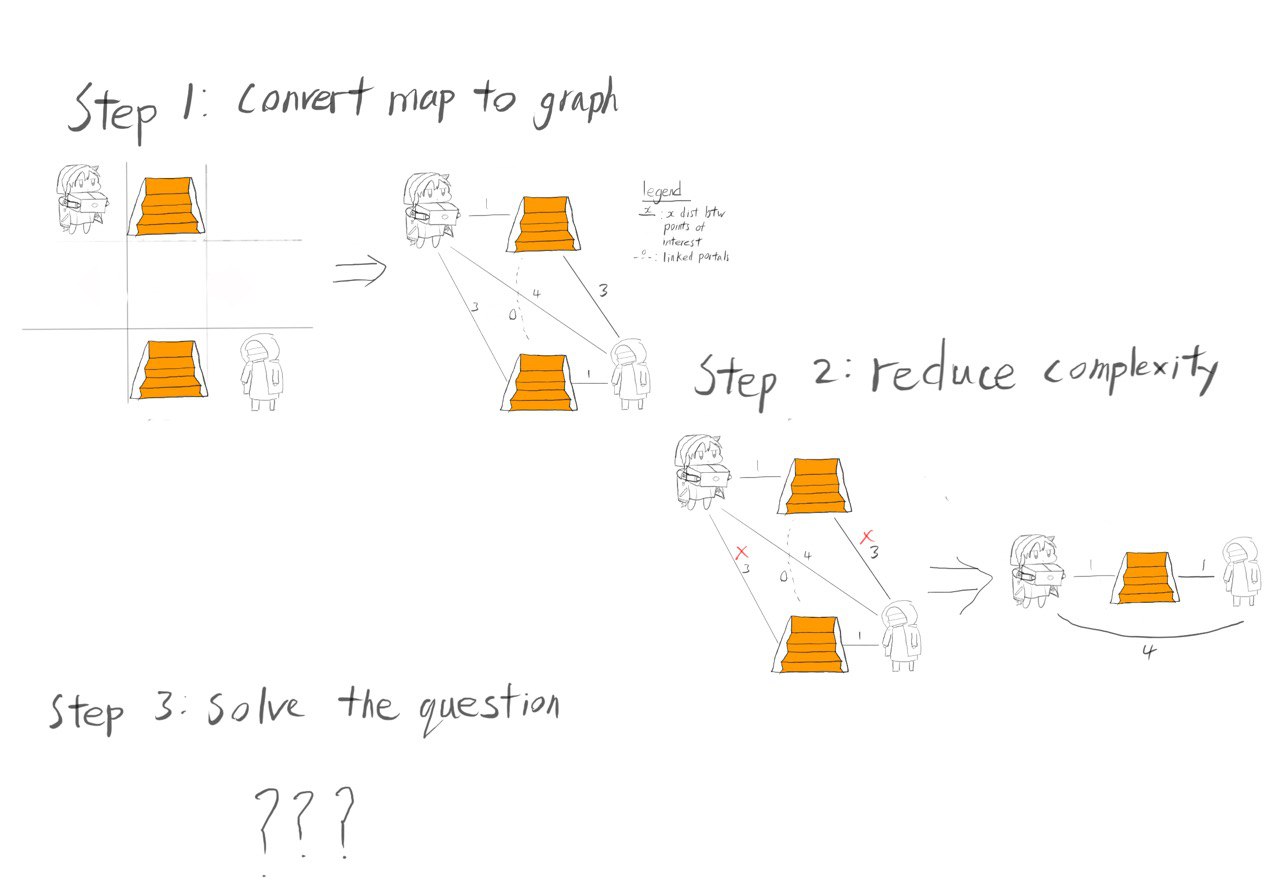
Dijkstra's algorithm
Finding the shortest distance:
The first step is to label the distant of each node from the start as the length of the edge connecting the node and the start. From there, each node is investigated systematically, in increasing distance from the start
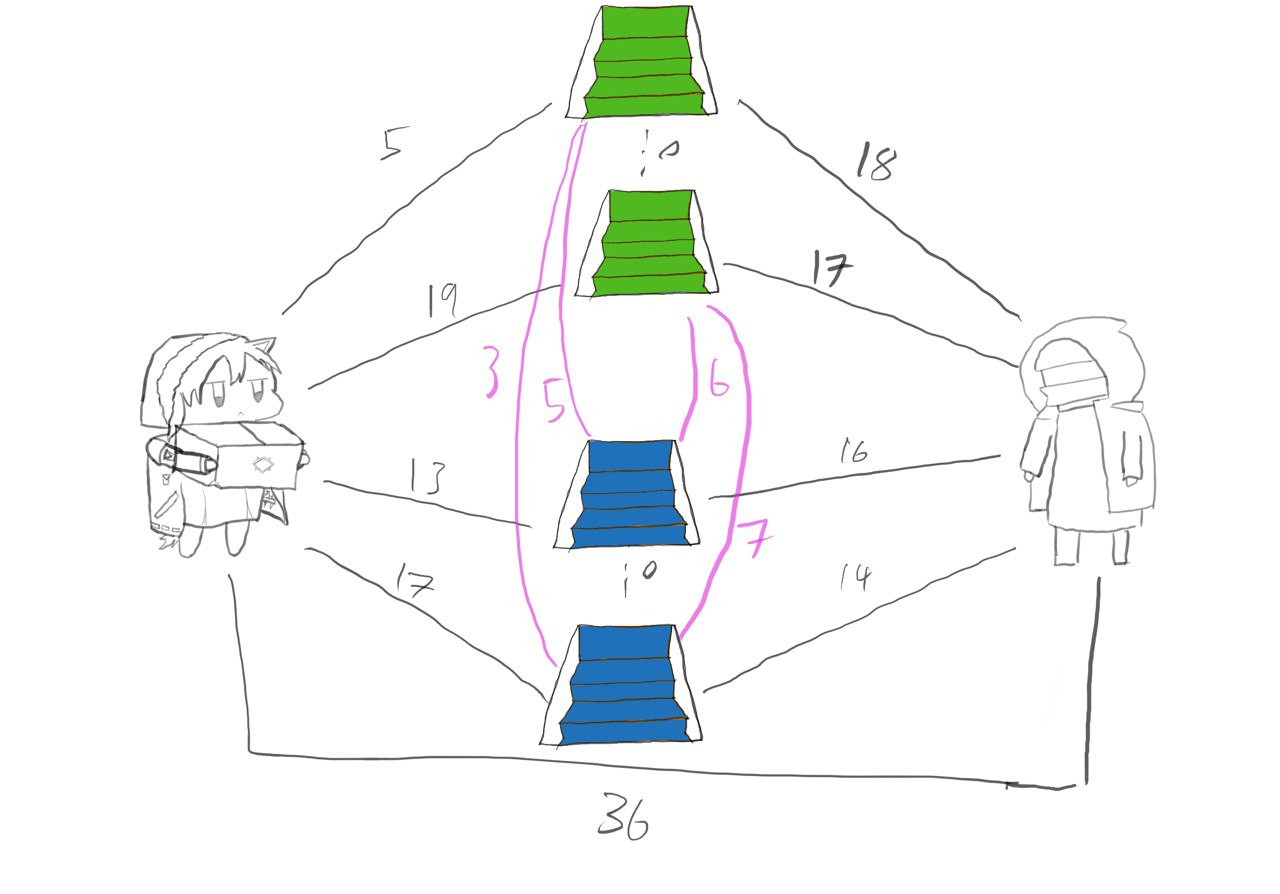
While a node is being investigated, if the total distance to another node is less than the initially labelled distance, the new distance and the route used is saved. Taking the 3 by 3 example matrix, if the sum of the distance from the start to portal 1 and portal 1 to the end is less than the distance from the start to the end, then the new optimal route is to go from start to portal 1 to the end.
Once every node has been investigated, the shortest distance from the start to the end will be discovered and give us our solution.
This file contains the bulk of the problem solving. Although the team waw unable to complete this program during the competition itself, it was completed after out of interest.
The program starts by storing the data in dictionaries, with each type of location being the key and the values being list of the [column, row] they were found in.
From there they were processed using the relative_positions functions, which takes the dictionary and returns a dictionary of the shortest distance between each of the nodes as well as the coordinates of the start and end point of the shortest path possible.
Using the dictionary of distances, the points were explored based on increasing distance and were then popped from the dictionary until every node was explored.
Once this was done for all the nodes, the distance from the start to the end was returned.
######################functions#########################
#returns an integer of number of steps between 2 points
from turtlegrid import arrow_drawer, grid
import turtle
def distance(list1, list2):
return abs(list1[0] - list2[0]) + abs(list1[1] - list2[1])
#receives twolist of everypoint of two types of points and finds the shortest distance between the two
def shortest_distance(list1, list2):
current_lowest = None
path = []
for location1 in list1:
for location2 in list2:
if current_lowest == None:
current_lowest = distance(location1, location2)
path = [location1, location2]
if distance(location1, location2) < current_lowest:
current_lowest = distance(location1, location2)
path = [location1, location2]
return current_lowest, path
#calculation of distance of all keypoints relative to one another
def relative_positions(config):
distance_chart = {}
path_chart = {}
for main_location in config:
main_location_positions = config.get(main_location)
distance_subchart = {}
path_subchart = {}
for sub_location in config:
if sub_location == main_location:
continue
sub_location_positions = config.get(sub_location)
distance_subchart[sub_location], path_subchart[sub_location] = shortest_distance(main_location_positions, sub_location_positions)
distance_chart[main_location] = distance_subchart
path_chart[main_location] = path_subchart
return distance_chart, path_chart
#receiving the config of the map and estab lishing key locations in a dictionary
layout = list(map(int, input().split())) #first number is column, second number is row
config = {}
config["S"] = [[0, 0]]
for y in range(layout[1]): #which row it is in
row = list(map(int, input().split()))
for x in range(layout[0]):
if row[x] == 0: #which column it is in
continue
#how to tell expected types
coordlist = config.get(row[x], [])
coordlist.append([x, y])
config[row[x]] = coordlist
config["E"] = [[layout[0] - 1, layout[1] - 1]]
print(config, layout)
distances, pathtakenalong = relative_positions(config)
#find distances from each kind of node from the start
distance_from_start = {'S': 0}
path_from_start = {}
for x in distances.get('S'):
distance_from_start[x] = distances.get('S').get(x)
path_from_start[x] = pathtakenalong.get('S').get(x)
distances.pop('S')
pathtakenalong.pop('S')
#iterate through the nearest point that remains unexplored and check if there are shorter connections to be made
#finding the point closest to the origin to explore first
while distances != {}:
available_explorations = []
for x in distances:
available_explorations.append(x)
point_to_explore = None
for x in available_explorations:
if point_to_explore == None:
point_to_explore = x
if distance_from_start.get(x) < distance_from_start.get(point_to_explore):
point_to_explore = x
point_dict = distances.get(point_to_explore)
for (x, y) in zip(point_dict.keys(), point_dict.values()):
if distance_from_start[point_to_explore] + y < distance_from_start[x]:
distance_from_start[x] = distance_from_start[point_to_explore] + y
path_from_start[x] = path_from_start.get(point_to_explore) + pathtakenalong.get(point_to_explore).get(x)
distances.pop(point_to_explore)
print(distance_from_start.get('E'))
print(path_from_start.get('E'))
turtle.setworldcoordinates(0, 0, 800, 800)
t1 = turtle.Turtle()
t1.speed(50)
t1.hideturtle()
grid(layout, config, t1)
arrow_drawer(path_from_start.get('E'),t1, layout)
turtle.done()
Another turtle program was created subsequently to create a visual representation of the answer in order to properly conclude the project (and also to convince myself that the path is indeed the shortest)
This program takes the path and layout found in the main program uses the turtles in order to create a drawing of the optimal path to be taken. It does this with Several functions:
converter: converts the config dictionary and swaps the keys and values
square and grid: Takes the layout and config file in order to draw the actual map first.
arrow: Which takes a final and initial position and draws horizontal and vertical lines to reach that point.
Code:
>import turtle
import random
def square(turtle, coordinates, scale, fillcolor):
#function to draw the individual squares
#takes fill color and coordinates(x,y)
turtle.penup()
turtle.goto( (coordinates[0])*scale, (coordinates[1]- 1)*scale )
turtle.pendown()
turtle.fillcolor(fillcolor)
turtle.begin_fill()
for i in range(4):
turtle.forward(1 * scale)
turtle.left(90)
turtle.end_fill()
def grid(layout, config, turtle):
special_slots, types = converter(config)
choosen_color = {}
for i in range(len(types)):
choosen_color[types[i]] = (random.randint(0, 255)/255, random.randint(0, 255)/255, random.randint(0, 255)/255 )
for i in range(layout[0]):
for j in range(layout[1]):
color = (0, 0 ,0)
if (i,j) in special_slots:
color = choosen_color.get(special_slots.get((i,j)))
square(turtle, [i, layout[1] - j], 100, color)
#function to draw the complete grid with the portals
#Takes in the input from the array and assigns random colour for the portals
#calls the squarre function and passes them the coordinate and colour of the portal to be drawn
def converter(config):
points = {}
type_points = []
for x in config.keys():
for y in config.get(x):
points[tuple(y)] = x
type_points.append(x)
return points, type_points
def arrow(turtle, initial, final, scale, layout):
#The function in order to draw the individual arrows
change = [final[0] - initial[0], final[1]- initial[1]]
turtle.penup()
turtle.goto( (initial[0] + 0.5)*scale, (layout[1] - initial[1] - 0.5)*scale)
turtle.pendown()
turtle.color(1,0,0)
if change[0] != 0:
turtle.left(change[0]/abs(change[0])*-90 + 90)
turtle.forward(scale* 0.5* abs(change[0]))
turtle.begin_fill()
turtle.left(150)
turtle.forward(scale*0.3)
turtle.left(120)
turtle.forward(scale*0.3)
turtle.left(120)
turtle.forward(scale*0.3)
turtle.end_fill()
turtle.right(30)
turtle.forward(scale* 0.5* abs(change[0]))
turtle.setheading(0)
if change[1] != 0:
turtle.left(change[1]/abs(change[1])* -90)
turtle.forward(scale* 0.5* abs(change[1]))
turtle.color(1,0,0)
turtle.begin_fill()
turtle.left(150)
turtle.forward(scale*0.3)
turtle.left(120)
turtle.forward(scale*0.3)
turtle.left(120)
turtle.forward(scale*0.3)
turtle.end_fill()
turtle.right(30)
turtle.forward(scale* 0.5* abs(change[1]))
turtle.setheading(0)
def arrow_drawer(path, turtle, layout):
for i in range(int(len(path)/2)):
arrow(turtle, path[i*2], path[i*2 + 1], 100, layout)
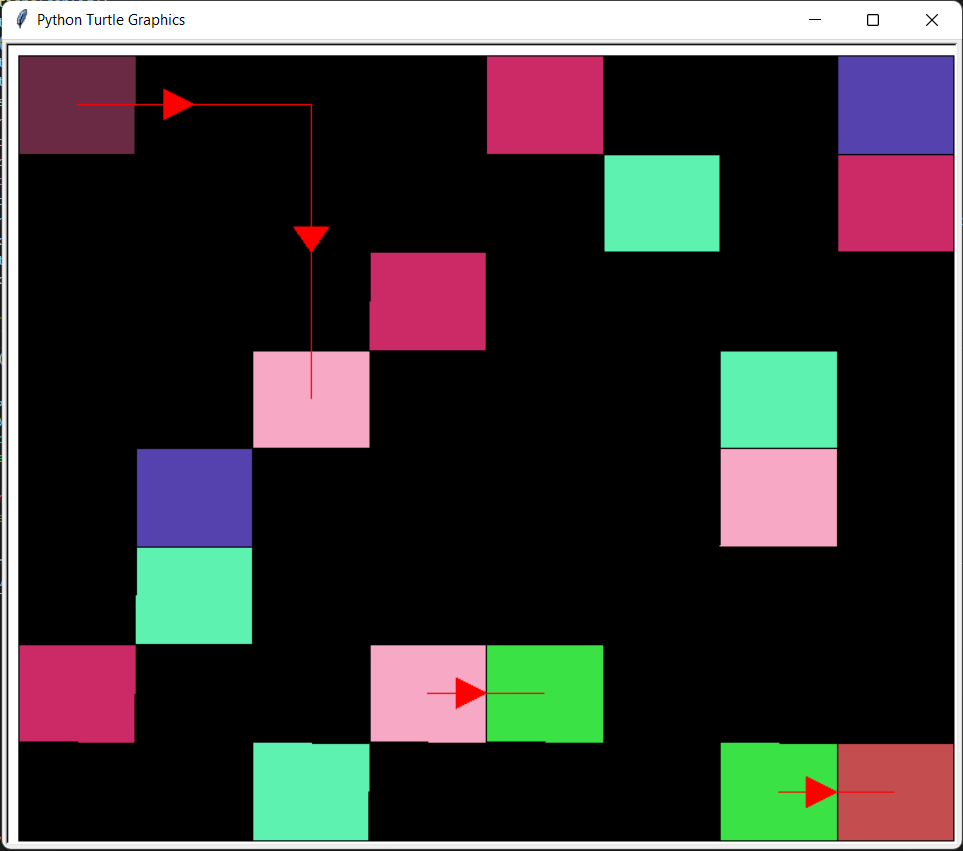
The computer solving an 8 by 8 matrix
1.Label the code
Specifically what the input and output of each function is. I finished the main code a while ago and when I returned to write the turtle code I spent a while trying to decode what the program was doing and how.
2. Documentation isn't easy
This page on the site took a day (specifically 9th April 2022) to create and really showed me how much thought goes into creating a site. Planning the page on Figma, creating the assets and implementing the page in HTML and CSS... But I am confident with more practice, I should be able to make these pages more efficiently and better in the future.
Error handling
The code right now has no error handling which can result in trouble being used
Dynamic website/compressed exe file
It would be great if the code could be hosted online on an active website based on something like react and be used like an online calcultaor. An interface could also be created in pyqt5 and compressed into a simple exe file.
Learn more about algorithms
I think one of the big reasons we were unable to finish the code for the competition was the large amount of time spent looking for algorithms and trying to comprehend them. Combined with having to think how to implement them in code and adapt them to the problem resulted in too much time being spent.
I think the project was a success and served as a great introduction to algorithm and I really enjoyed the challenge of creating an elegant solution to tackle the situation. There are so many areas that this project and the journey on machine learning can go from here and I am eager to continue learning more.